Skip to content
Menu
Technical University of Munich
Technical University of Munich

Numerical methods for simulating quantum systems

Our expertise is in tensor network and quantum Monte Carlo methods, and we are also exploring neural network quantum states. For example, we have implemented matrix-product-operator techniques to study out-of-time ordered correlation (OTOC) functions and elucidate scrambling of quantum information, and have applied the determinant quantum Monte Carlo (DQMC) algorithm to a three-band Hubbard model of high-Tc cuprate superconductors.

Selected publications and preprints:

Selected software projects:

  • ChemTensor
    C implementation of tensor network data structures and algorithms tailored towards simulating chemical systems (work in progress)

  • PyTreeNet
    Python implemention of tree tensor networks with a focus on the simulation of quantum systems admitting a tree topology

  • PyTeNet
    Quantum tensor network operations and simulations based on matrix product states

Quantum algorithms

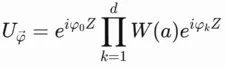
We explore and investigate algorithms for "quantum simulation", i.e., using a quantum computer to simulate a target quantum system, like a (strongly correlated) system in condensed matter physics or chemistry. In particular, we study approaches based on qubitization and the quantum singular value transform, as well as embedding frameworks like DMET. We also investigate quantum algorithms for optimization and machine learning.

Selected publications and preprints:

IBM's 50-qubit quantum computer

Quantum computing software stack

Currently we are working on a Python package qib  (still early stage) for translating high-level quantum algorithms to circuits and submitting these to hardware backends. We also investigate hybrid quantum-classical programming languages and runtime environments.

Selected publications and preprints:

  • Amr Elsharkawy, Xiao-Ting Michelle To, Philipp Seitz, Yanbin Chen, Yannick Stade, Manuel Geiger, Qunsheng Huang, Xiaorang Guo, Muhammad Arslan Ansari, Christian B. Mendl, Dieter Kranzlmüller, Martin Schulz
    Integration of quantum accelerators with high performance computing - A review of quantum programming tools
    arXiv:2309.06167

Selected software projects:

  • MILQ
    Quantum scheduler

  • rqcopt
    Riemannian quantum circuit optimization

  • qib - quantum library
    Python package for quantum circuits and algorithms

Statistical physics and generalized hydrodynamics

Together with Herbert Spohn, we investigate statistical physics models of one-dimensional systems, elucidating anomalous transport properties and detailed connections to KPZ theory. We support the theory by numerical molecular dynamics simulations.

Selected publications and preprints:

To top