Graph Posterior Network: Bayesian Predictive Uncertainty for Node Classification
This page is about our paper
Graph Posterior Network: Bayesian Predictive Uncertainty for Node Classification
by Maximilian Stadler*, Bertrand Charpentier*, Simon Geisler, Daniel Zügner and Stephan Günnemann
Published at the Neural Information Processing Systems (Neurips) 2021
Abstract
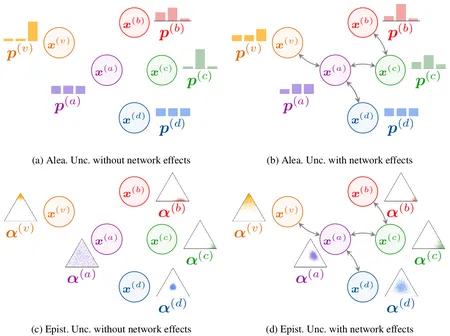
The interdependence between nodes in graphs is key to improve class predictions on nodes and utilized in approaches like abel Propagation (LP) or in Graph Neural Networks (GNNs). Nonetheless, uncertainty estimation for non-independent node-level predictions is under-explored. In this work, we explore uncertainty quantification for node classification in three ways: (1) We derive three axioms explicitly characterizing the expected predictive uncertainty behavior in homophilic attributed graphs. (2) We propose a new model Graph Posterior Network (GPN) which explicitly performs Bayesian posterior updates for predictions on interdependent nodes. GPN provably obeys the proposed axioms. (3) We extensively evaluate GPN and a strong set of baselines on semi-supervised node classification including detection of anomalous features, and detection of left-out classes. GPN outperforms existing approaches for uncertainty estimation in the experiments.