Generalizing Neural Wave Functions
by Nicholas Gao and Stephan Günnemann
Published at the 40th International Conference on Machine Learning (ICML), 2023
Abstract
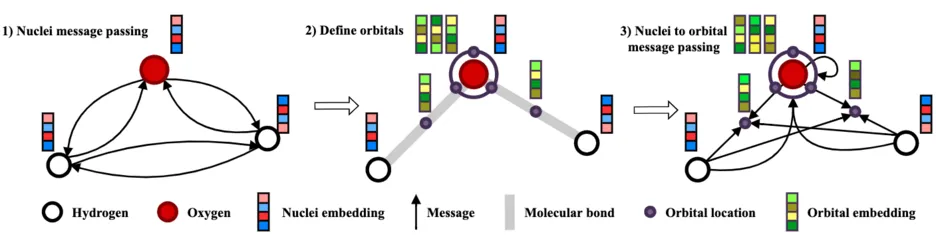
Recent neural network-based wave functions have achieved state-of-the-art accuracies in modeling ab-initio ground-state potential energy surface. However, these networks can only solve different spatial arrangements of the same set of atoms. To overcome this limitation, we present Graph-learned orbital embeddings (Globe), a neural network-based reparametrization method that can adapt neural wave functions to different molecules. By connecting molecular orbitals to covalent bonds, Globe learns representations of local electronic structures that generalize across molecules via spatial message passing. Further, we propose a size-consistent wave function Ansatz, the Molecular orbital network (Moon), tailored to solving Schrödinger equations of different molecules jointly. In our experiments, we find Moon requires 4.5 times fewer steps to converge to similar accuracy as previous methods and to lower energies given the same time. Further, our analysis shows that Moon's energy estimate scales additively with increased system sizes, unlike previous work where we observe divergence. In both computational chemistry and machine learning, we are the first to demonstrate that a single wave function can solve the Schrödinger equation of molecules with different atoms jointly.
Cite
Please cite our paper if you use the model, experimental results, or our code in your own work:
@inproceedings{gao_globe_2023,
title = {Generalizing Neural Wave Functions},
author = {Gao, Nicholas and G{\"u}nnemann, Stephan},
booktitle={International Conference on Machine Learning (ICML)},
year = {2023}
}