Learning the Dynamics of Physical Systems from Sparse Observations with Finite Element Networks
Links
Abstract
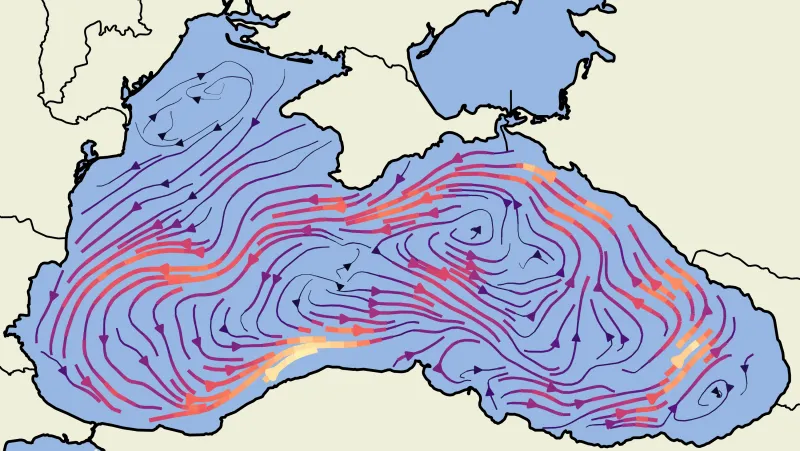
We propose a new method for spatio-temporal forecasting on arbitrarily distributed points. Assuming that the observed system follows an unknown partial differential equation, we derive a continuous-time model for the dynamics of the data via the finite element method. The resulting graph neural network estimates the instantaneous effects of the unknown dynamics on each cell in a meshing of the spatial domain. Our model can incorporate prior knowledge via assumptions on the form of the unknown PDE, which induce a structural bias towards learning specific processes. Through this mechanism, we derive a transport variant of our model from the convection equation and show that it improves the transfer performance to higher-resolution meshes on sea surface temperature and gas flow forecasting against baseline models representing a selection of spatio-temporal forecasting methods. A qualitative analysis shows that our model disentangles the data dynamics into their constituent parts, which makes it uniquely interpretable.
Cite
@inproceedings{lienen_fen2022,
title = {Learning the Dynamics of Physical Systems from Sparse Observations with Finite Element Networks},
author = {Lienen, Marten and G\"unnemann, Stephan},
booktitle={International Conference on Learning Representations (ICLR)},
year = {2022},
}