Equivariance Robustness

This page links to additional material for our paper

Provable Adversarial Robustness for Group Equivariant Tasks: Graphs, Point Clouds, Molecules, and More
by Jan Schuchardt, Yan Scholten, and Stephan Günnemann
Published at Neural Information Processing Systems (NeurIPS) 2023

Links

[Paper | Poster | Github]

Abstract

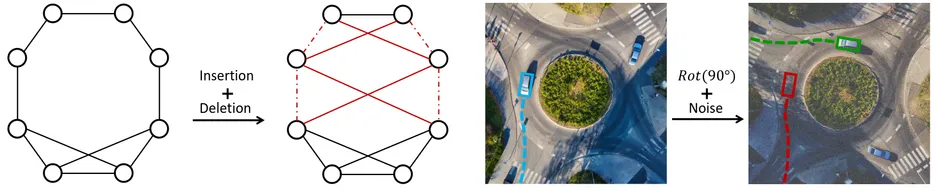
A machine learning model is traditionally considered robust if its prediction remains (almost) constant under input perturbations with small norm. However, real-world tasks like molecular property prediction or point cloud segmentation have inherent equivariances, such as rotation or permutation equivariance. In such tasks, even perturbations with large norm do not necessarily change an input's semantic content. Furthermore, there are perturbations for which a model's prediction explicitly needs to change.
For the first time, we propose a sound notion of adversarial robustness that accounts for task equivariance. We then demonstrate that provable robustness can be achieved by (1) choosing a model that matches the task's equivariances (2) certifying traditional adversarial robustness. Certification methods are, however, unavailable for many models, such as those with continuous equivariances. We close this gap by developing the framework of equivariance-preserving randomized smoothing, which enables architecture-agnostic certification. We additionally derive the first architecture-specific graph edit distance certificates, i.e. sound robustness guarantees for isomorphism equivariant tasks like node classification. Overall, a sound notion of robustness is an important prerequisite for future work at the intersection of robust and geometric machine learning.

Cite

Please cite our paper if you use the method in your own work:

@InProceedings{Schuchardt2023_Equivariance,
author = {Schuchardt, Jan and Scholten, Yan and G{\"u}nnemann, Stephan},
title = {Provable Adversarial Robustness for Group Equivariant Tasks: Graphs, Point Clouds, Molecules, and More},
booktitle = {Conference on Neural Information Processing Systems (NeurIPS)},
year = {2023}
}