Design and Optimization of Functionally-graded Triangular Lattices for Multiple Loading Conditions

Junpeng Wang¹, Rüdiger Westermann¹, Xifeng Gao², Jun Wu³

1 Chair of Computer Graphics and Visualization, Technical University of Munich, Germany

2 Lightspeed Studios, Bellevue, WA, USA

3 Delft University of Technology, Delft, 2628 CE, The Netherlands

Abstract

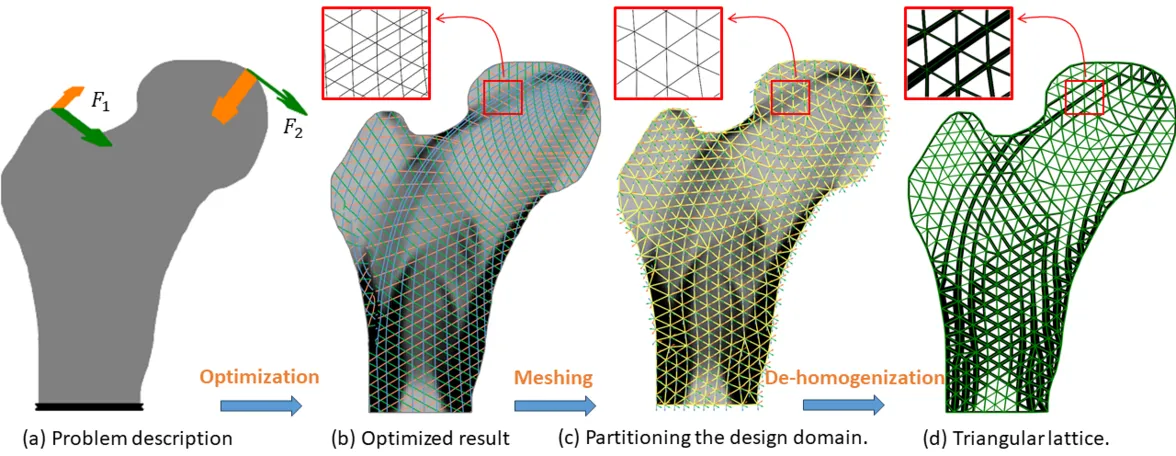
Aligning lattices based on local stress distribution is crucial for achieving exceptional structural stiffness. However, this aspect has primarily been investigated under a single load condition, where stress in 2D can be described by two orthogonal principal stress directions. In this paper, we introduce a novel approach for designing and optimizing triangular lattice structures to accommodate multiple loading conditions, which means multiple stress fields. Our method comprises two main steps: homogenization-based topology optimization and geometry-based de-homogenization. To ensure the geometric regularity of triangular lattices, we propose a simplified version of the general rank-$3$ laminate and parameterize the design domain using equilateral triangles with unique thickness per edge. During optimization, the thicknesses and orientation of each equilateral triangle are adjusted based on the homogenized properties of triangular lattices. Our numerical findings demonstrate that this proposed simplification results in only a slight decrease in stiffness of less than 5% compared to using the general rank-3 laminate, while achieving triangular lattice structures with a compelling geometric regularity. In geometry-based de-homogenization, we adopt a field-aligned triangulation approach to generate a globally consistent triangle mesh, with each triangle oriented according to the optimized orientation field. Our approach for handling multiple loading conditions, akin to de-homogenization techniques for single loading conditions, yields highly detailed, optimized, spatially varying lattice structures. The method is computationally efficient, as simulations and optimizations are conducted at a low-resolution discretization of the design domain. Furthermore, since our approach is geometry-based, obtained structures are encoded into a compact geometric format that facilitates downstream operations such as editing and fabrication.

Associated publications

Design and Optimization of Functionally-graded Triangular Lattices for Multiple Loading Conditions
Junpeng Wang, Rüdiger Westermann, Xifeng Gao, Jun Wu
Computer Methods in Applied Mechanics and Engineering, 2024
[Preprint]