Visualizing the Central Tendency of Ensembles of Shapes
Ismail Demir, Mihaela Jarema, Rüdiger Westermann
Computer Graphics and Visualization Group, Technische Universität München, Germany
Background
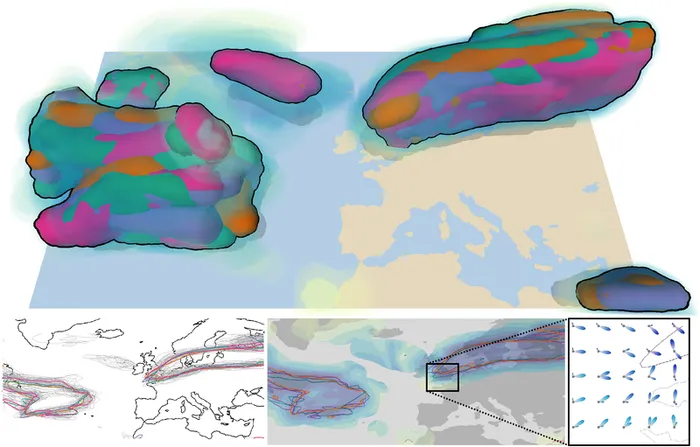
We propose a new approach for analyzing the central tendency (centrality) of an ensemble of shapes in 2D or 3D space. Our approach provides means to determine the most central shape from a given set of shapes, to quantify the region-wise centrality of the shapes, and to compute a locally most representative shape. Unlike previous approaches, which build upon binary functions or signed distance fields to locate domain points with respect to orientable shapes, we introduce a closest point representation for the analysis of ensembles of shapes. By using this representation, our approach can handle arbitrary non-parametric shapes regardless of dimension and orientability. Shapes are first converted into an implicit representation based on vectors to closest surface points, and the resulting directional distributions are then used to perform region-wise classifications. Shapes are either analyzed separately by evaluating the classifications over the shape, or additional fields are derived from these classifications, in which specific shapes like the locally best mean are given as level-sets. We demonstrate the effectiveness of our approach on synthetic and weather forecast ensembles in 2D and 3D.
Acknowledgement
Access to ECMWF prediction data has been kindly provided in the context of the ECMWF special project "Support Tool for HALO Missions". We are grateful to the special project members Marc Rautenhaus and Andreas Dörnbrack for providing the ECMWF ENS dataset of 17 October 2012. This work was supported by the European Union under the ERC Advanced Grant 291372 - SaferVis - Uncertainty Visualization for Reliable Data Discovery.