Visualizing the Positional and Geometrical Variability of Isosurfaces in Uncertain Scalar Fields

Tobias Pfaffelmoser, Matthias Reitinger, Rüdiger Westermann
Computer Graphics and Visualization Group, Technische Universität München, Germany

Background

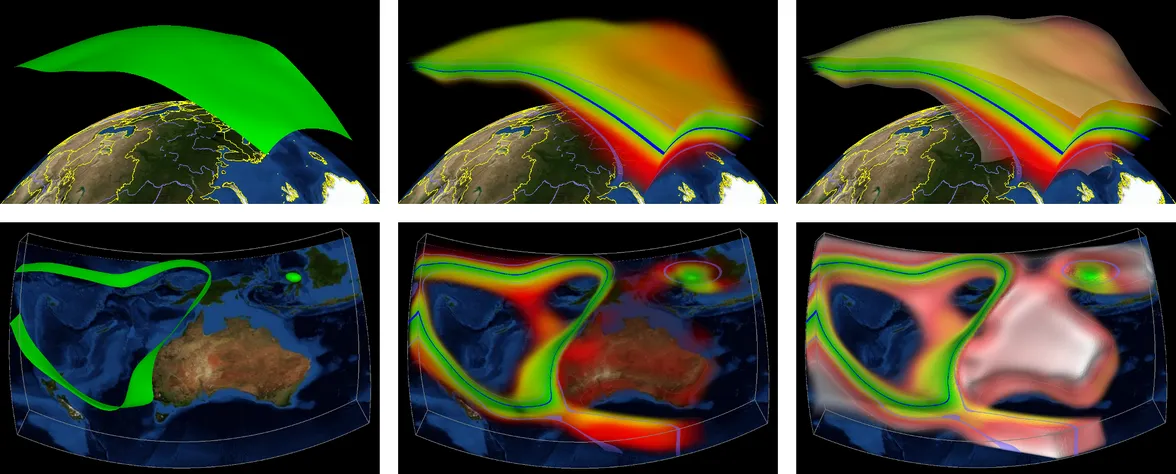
We present a novel approach for visualizing the positional and geometrical variability of isosurfaces in uncertain 3D scalar fields. Our approach extends recent work by Pöthkow and Hege in that it accounts for correlations in the data to determine more reliable isosurface crossing probabilities. We introduce an incremental update-scheme that allows integrating the probability computation into front-to-back volume ray-casting efficiently. Our method accounts for homogeneous and anisotropic correlations, and it determines for each sampling interval along a ray the probability of crossing an isosurface for the first time. To visualize the positional and geometrical uncertainty even under viewing directions parallel to the surface normal, we propose a new color mapping scheme based on the approximate spatial deviation of possible surface points from the mean surface. The additional use of saturation enables to distinguish between areas of high and low statistical dependence. Experimental results confirm the effectiveness of our approach for the visualization of uncertainty related to position and shape of convex and concave isosurface structures.

A preprint of the article is available for download below. The definitive version is available at http://diglib.eg.org and http://onlinelibrary.wiley.com.

Acknowledgments

The first author is funded by the Munich Centre for Advanced Computing and the International Graduate School of Science and Engineering (IGSSE) at the Technische Universität München.

Associated Publications

Visualizing the Positional and Geometrical Variability of Isosurfaces in Uncertain Scalar Fields
T. Pfaffelmoser, M. Reitinger, R. Westermann, 
Computer Graphics Forum (Proceedings of EuroVis 2011) [Download] [Bibtex]